Introduction

The most common Encryption methods used on the internet are RSA (Rivest, Shamir, and Adleman) and ECC (Elliptic Curve Cryptography).These Encryption methods are used to Encrypt the data sent over the Internet, classical computers cant break these encryption in any meaningful time frame but Quantum Computers can lets see how.

How Modern Encryption works

In general, you have a private key and a public key, the sender encrypts a message using the recipient’s public key, and only the recipient can decrypt it using their private key.

RSA

In RSA, the security is based on the difficulty of factoring large composite numbers into their prime factors. While multiplying two large prime numbers is computationally simple, reversing the process is extremely difficult for classical computers, especially as the size of the numbers increases.

1. Key Generation

• Step 1: Choose two large prime numbers (p and q).

• Step 2: Multiply them to get a large number n (n = p × q). This will be part of both the public and private keys.

• Step 3: Calculate a special number φ(n) (which is (p-1) × (q-1)).

• Step 4: Choose a small public exponent e (often 65537) that is coprime with φ(n).

• Step 5: Compute the private key d, which is the inverse of e mod φ(n).

Now, you have:

• Public key (n, e) – anyone can see this.

• Private key (n, d) – this is secret and known only to the owner.

2. Encryption

• The sender takes a message (converted into a number m) and uses the recipient's public key (n, e) to encrypt it.

• The ciphertext is calculated as:

  Ciphertext (c) = m^e mod n

3. Decryption

• The recipient, who has the private key (n, d), can decrypt the ciphertext.

• The original message is recovered by:

  Message (m) = c^d mod n

  

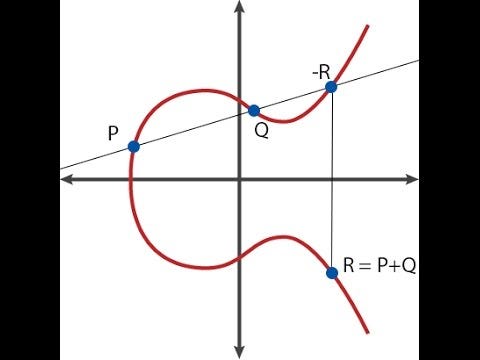
ECC

In ECC, security is based on the difficulty of solving the Elliptic Curve Discrete Logarithm Problem (ECDLP). While it is computationally straightforward to perform scalar multiplication on an elliptic curve—multiplying a point by a large integer to get another point—reversing this process, that is, finding the scalar given the two points, is extremely difficult for classical computers. As the size of the elliptic curve key increases, the difficulty of solving ECDLP grows exponentially, making it infeasible to break ECC with classical algorithms.

1. Key Generation

• Step 1: Choose an elliptic curve equation and a base point P (a predefined point on the curve).

• Step 2: Select a random private key k (a large integer).

• Step 3: Calculate the public key by performing scalar multiplication of the base point P by the private key k:

  • PublicKey = Q = k×P

Now, you have:

• Private Key k: A large random number (kept secret).

• Public Key Q: A point on the elliptic curve (shared publicly).

2. Encryption

• Step 1: The sender retrieves the recipient’s public key Q and chooses a random integer r.

• Step 2: The sender calculates two points:

  • R = r × P (this will be part of the ciphertext).

  • A shared secret S = r × Q (used to encrypt the message).

• Step 3: The message mmm (converted into a number) is encrypted using the shared secret SSS.

  • The ciphertext consists of two parts: (R, EncryptedMessage), where EncryptedMessage = m + S.

3. Decryption

• Step 1: The recipient uses their private key k to compute the shared secret S from the received point R:

  • S = k × R

• Step 2: The recipient subtracts the shared secret S from the encrypted message to retrieve the original message m:

  • Message = EncryptedMessage − S

    

Why Quantum Computers can break encryption

The reason quantum computers can break both RSA and ECC is not just faster computation—it’s the nature of quantum algorithms like Shor’s. Classical cryptographic systems are designed around problems that are hard to reverse (like factoring and discrete logarithms), but quantum computers, using properties like superposition and entanglement, can explore many possibilities simultaneously and find solutions much more efficiently.

• Superposition allows qubits to exist in multiple states simultaneously, performing multiple calculations at once.

• Entanglement provides a way to link qubits such that changes to one instantaneously affect the others, allowing faster data processing.

• Shor’s Algorithm leverages these quantum properties to dramatically reduce the time complexity for factoring and solving discrete logarithms, fundamentally undermining the security assumptions of RSA and ECC.

Breaking RSA

RSA encryption is based on the difficulty of factoring large composite numbers into their prime factors. While classical computers take an infeasibly long time to factor numbers that are hundreds or thousands of digits long, Shor's algorithm changes this dramatically.

How Quantum Computing Exploits RSA:

• Factoring as the Core Weakness: RSA encryption uses two large prime numbers, p and q, to create a public key n = p × q. The security of RSA lies in the fact that no known classical algorithm can factor n efficiently.

• Shor’s Algorithm: Quantum computers can use Shor’s algorithm to factor nnn in polynomial time. This is exponentially faster than the best-known classical methods, such as the General Number Field Sieve, which take super-polynomial time.

Once the quantum computer factors n into p and q, it can easily compute the private key using the relationship between p, q, and the public exponent e.

Breaking RSA

Elliptic Curve Cryptography (ECC) relies on the difficulty of solving the Elliptic Curve Discrete Logarithm Problem (ECDLP). The problem: given a public point Q=k×P (where P is a known base point and k is a secret scalar), finding k is computationally infeasible for classical computers.

How Quantum Computing Exploits ECC:

• ECDLP as the Core Weakness: In ECC, the discrete logarithm problem on elliptic curves is assumed to be computationally hard because classical algorithms take an infeasible amount of time to reverse the scalar multiplication (finding k from Q and P).

• Shor’s Algorithm: Quantum computers can use Shor’s algorithm to solve the ECDLP in polynomial time. Essentially, Shor's algorithm can compute the discrete logarithm just as efficiently as it factors integers, making ECC encryption vulnerable to quantum attacks.

Once a quantum computer solves the discrete logarithm problem and kinds k, it can derive the private key from the public key and decrypt any encrypted communication.

Current Solutions:

The National Institute of Standards and Technology (NIST) has proposed four encryption algorithms for post-quantum cryptography, which are designed to be secure against attacks by quantum computers. These algorithms were selected after a multi-year competition to identify quantum-resistant encryption standards. Out of the 4, 3 are based on Lattice-based cryptography.

Lattice based Cryptography

Lattice-based encryption is a type of cryptography that uses mathematical grids (called lattices) to create secure encryption schemes. These lattices are like multi-dimensional grids, where encryption and decryption operations happen.

Its Workings

1. Lattices: Grids in High Dimensions

• Imagine a 2D grid made of points. Now, think of this grid expanding into many more dimensions—this is a lattice.

• The positions of the points in these high-dimensional lattices are used to create complex mathematical problems.

2. The Encryption Process

• In lattice-based encryption, messages are transformed into points within this high-dimensional grid.

• The key idea is to "hide" the message in the lattice by adding random noise or errors. The encrypted message is a point close to the correct message, but slightly off due to the noise.

3. Why It's Secure

• The core problem in lattice encryption is finding the shortest vector or solving the Learning With Errors (LWE) problem. This is like trying to find the closest point on the lattice while dealing with the added noise.

• Even quantum computers struggle with these problems because the noise makes it extremely difficult to reverse-engineer the original message without the private key.

4. Decryption

• The person with the private key knows how to remove the noise and find the correct point (the original message) in the lattice.

  

Why Lattice-Based Encryption is Strong

The difficulty of finding the right point in a high-dimensional lattice, especially with noise, makes this form of encryption resistant to attacks by both classical and quantum computers. Because these problems are extremely hard to solve, even with quantum computing, lattice-based encryption is considered quantum-safe and a promising option for future cryptographic standards.